
On the subject of radical interdisciplinary design, we discussed in class the fusion of music and engineering, something I’m sure we will see posts about in the upcoming days. What I would like to talk about is the fusion of two disciplines which I have personally spent a lot of time thinking about before vital ideation, and am really excited to share with others. At first glance pedagogy and digital communications seem to have little in common. In fact, the notion of pedagogical research going hand in hand with network signaling and digital communications research seems outlandish and foreign at best. The thing is, any two disciplines must overlap in potentially powerful ways, and these two are no exception.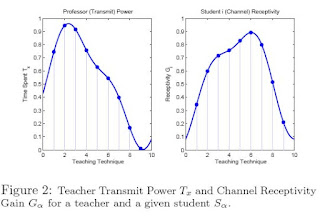
You can see from Figure 1 that the transmitter/receiver model is at least at a very basic level analogous to a teacher/student model where a lesson is transmitted to a student via some sort of signal. In this model a student’s receptivity to lesson X is based off their receptivity to specific teaching techniques. These techniques are used to varying degrees by a teacher, which can be depicted as the power spectral density of said teacher/transmitter’s transmit power, which in turn represents the amount of time teachers spend using a specific type of teaching technique. Figure 2 is a visual way to represent this last paragraph. You can see from the graph on the left, which shows professor “transmit” power as a function of the amount of time (shown on the vertical axis) they spend covering any material using different teaching techniques (shown on the horizontal axis.) Likewise the graph on the right shows student receptivity to different teaching techniques.
What a mouthful. To attempt to explain how this model might be useful, we consider the simple case of 30 students and a choice between two possible teaching techniques, Qa = Auditory Learning and Qb = Visual Learning. You can plot a student’s receptivity to these two teaching “techniques” on a two dimensional grid, where one axis is Qa and the other is Qb. The axes would range from 0->1 for each technique, where 1 is the hypothetical scenario were you as a student understand EVERYTHING that you learn using a specific technique. The ideal student would of course have a receptivity of 1 for both these values, but that wouldn’t make our model useful. The vector G1 would represent the 2-D vector representing these two student receptivities. We can create 30 students with randomly generated receptivity vectors [G1, G2, …G30] such that each student’s total receptivity||G|| is within an arbitrarily-defined range such as 0.3 < || G|| <>
Now, in the digital communications world you represent the power spectral density of a signal by multiplying the transmit power and channel receptivity. For us this means that in order to determine amount learned we can multiply the learning technique time distribution vector (in our 2-d example) for a professor by a student’s receptivity vector (for the two techniques) to give the amount “received as a signal” by a student from each “technique” The sum of the area under this student curve is the “amount learned”!
I will conclude the following post with an explanation of the following figure, which shows the example case of our 30 randomly generated students and the imaginary teacher who hypothetically could teach them any possible range of two specific techniques. What this translates to in the end is the following choice for a teacher: How much time do I spend say, watching videos as opposed to lecturing? Now, this case is obviously ideal because we can’t assume that we will know the exact “receptivity” of each student to a specific technique, and that this directly translates to amount learned, but in this end this is just a model of a teacher/student system. Every model is broken right? The only perfect model of a classroom environment is the classroom itself!
Each parabola shown in the figure above represents the projected learning efficiency E for a given student across the different mixes of auditory and visual learning techniques output by a professor. The vertex of each parabola corresponds to the student being taught by a teaching style that most perfectly matches his(her) receptivity Gn This value corresponds to the mix that represents that student’s highest learning efficiency. If we were teaching only one student, we would therefore choose the Auditory-Visual mix to coincide with the student’s vertex in this plot. However, we must teach to the entire class; so how can we select the direction of Tx? If our goal were to teach at a rate that did not exceed any student’s learning efficiency, the plot above implies that we should select about an equal mix of Auditory and Visual techniques, and we should choose a teaching rate (i.e. learning efficiency) of approximately 0.27. Qualitatively speaking, this corresponds to the highest learning efficiency in the plot that is below every parabola (or, the teaching rate below every student’s maximum learning efficiency). Instead of choosing this “lowest common denominator” approach, we may elect to forgo the few students with the lowest receptiveness in order to increase our teaching rate. Based on our understanding of the figure, any intelligent selection will exist at either the intersection of two parabolas or at the vertex of a parabola. We therefore limit our search to these points. You could envision a graph where you highlight only these two types of points and as you eliminate students you would move further up on the graph and around to different points to maximize the learning efficiency for the remaining N students.
The process for choosing this path up the graph can also be described intuitively as follows. Imagine you pressed a single finger up from the bottom of the last image shown. It would naturally center itself at the highest vertex or parabola union, which corresponds to the teaching technique mix (and the maximum learning efficiency threshold) that you would use to teach all 30 students. Next, say you wanted to exceed this threshold; you would effectively “ignore” one of the lowest parabolas and move to the next highest available point. This would be akin to teaching above the maximum learning efficiency for one of your students. This allows your technique mix to adjust itself to find the next maximum point. We can also plot the learning efficiency threshold height as a function of the number of students above the threshold; as discussed above, you can expect the maximum available threshold to increase as the number of students above the threshold decreases. With one student, assuming of course that our professor can transmit something perfect to that student’s receptivities, you achieve a learning efficiency of 1. With a decreased number of students under the threshold you achieve a lower perfect teaching efficiency for those students.
You could envision a scenario in this model where you chose your teacher signal at a point along this “path” up the vertexes and parabola union points that would maximize the overall amount of learning in the classroom. The “perfect learning efficiency” model up to this point hasn’t taken into account the fact that in the end the choice of a teacher’s T vector will lie somewhere on the 2-D student receptivity space for each student, and that on this space each student has their own perfect learning receptivity point. A teacher wanting to optimize his signal output would first decide an acceptable threshold for student learning, and then determine which of these points minimizes the distance between all the students he(she) is trying to teach for.
I welcome others to come up with two other seemingly random disciplines and merging them together somehow! I'm sure you can think of something in a quick 10 minutes. The basic idea for this post came about after a discussion asking the question "What if all knowledge could be plotted on a n-dimensional grid?" Without meaning to this successfully put linear algebra and digital communications in the same discussion space as pedagogy and learning. There are many more questions where this one came from, the real question is, do you ask yourself silly questions often enough to find real value in some of them?

No comments:
Post a Comment